Linear Regression

Linear Regression

공부 시간에 따른 성적에 대한 데이터를 가지고 지도 학습을 한다고 가정한다.

사전에 수집한 성적이라는 “정답”이 존재하므로 “supervised learning”에 해당하며, 추정하고자 하는 값이 실수값이므로 regression problem이다. 여기에 성적과 공부 시간 사이에 선형의 관계가 존재한다고 가정하면 Linear regression이 되는 것이다.

Hypothesis

Hypothesis 란, input (feature)과 output (target) 의 관계를 나타내는 함수이다.

선형 회귀에서는 다음과 같은 선형 함수를 자주 사용한다.

\[H(x) = Wx +b\]

우리의 목표는 여러가지 W와 b를 시도하여 평면 상에서 주어진 데이터 좌표들에 가장 잘 맞는, 혹은 그 점들을 가장 잘 대표하는 직선을 찾아내는 것이다.

Cost function

우리가 세운 가설과 실제 데이터가 얼마나 다른지 판단하기 위해서 Cost function을 사용한다.

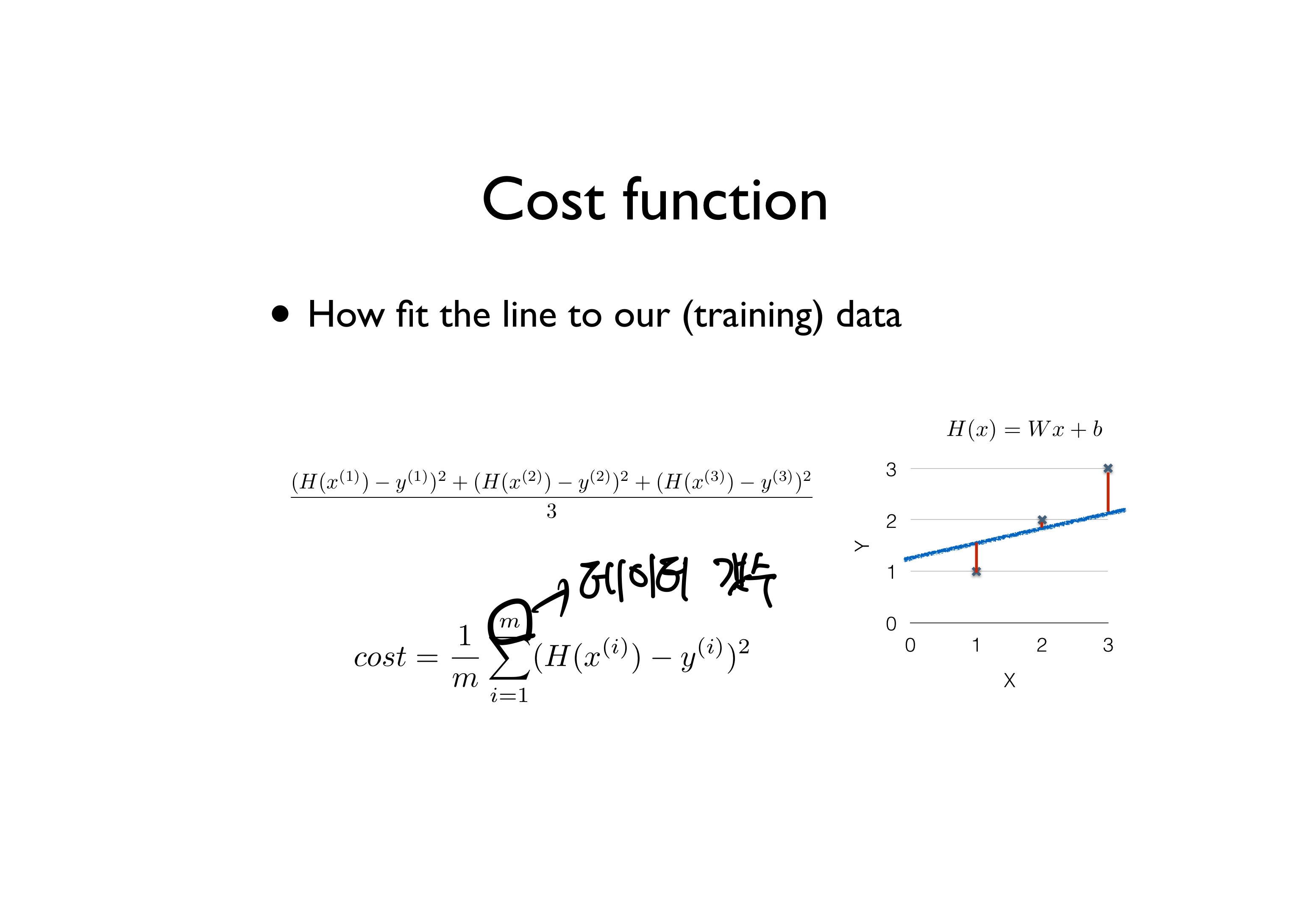
M개의 데이터에 대해 우리가 예측한 값과 실제값의 차이를 제곱하여 데이터의 수로 나누어준다.

cost funtion 일반화

\[cost = {1\over m }\displaystyle\sum_{i=1}^{m}(H(x^{(i)}-y^{(i)})^2\\ H(x)=Wx+b\\ \\ cost(W,b)={1\over m}\displaystyle\sum_{i=1}^{m}(H(x^{(i)}-y^{(i)})^2\]

Gradient descent algorithm

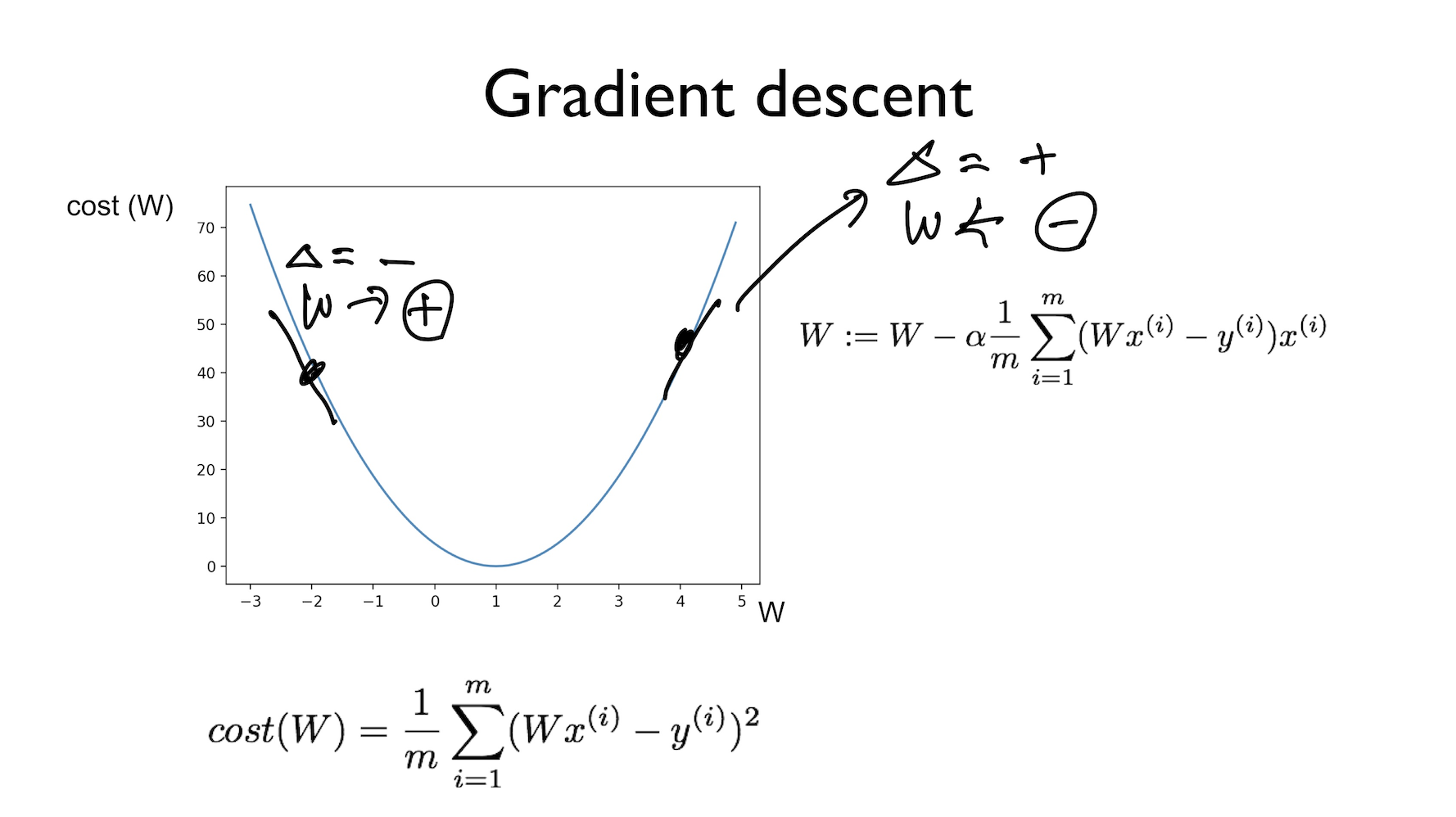
Gradient descent는 cost function을 최소화하기 위해 이용할 수 있는 방법 중 하나이며, cost function 말고도 각종 optimization에 이용되는 일반적인 방법이다.

함수의 기울기를 이용해 x의 값을 어디로 옮겼을 때 함수가 최소값을 찾는지 알아보는 방법이다

1. start at 0,0 (아무 지점에서나 시작 가능)
2. W를 변화한다
3. 경사도를 계산해서 다시 W를 변화시킨다.

경사도 계산을 위한 미분

\[{1\over 2m }\displaystyle\sum_{i=1}^{m}(Wx^{(i)}-y^{(i)})^2\\W : = W-\alpha* {\partial\over W \partial}cost(W)\]

​

Multi-Variable Linear Regression

X값이 여러개인 경우

변수가 많아질 수록 복잡해지는 문제가 발생한다.

이러한문제를 해결하기 위해서 Matrix multiplication을 사용한다

Matrix 를 사용하면 각각의 인스턴스를 계산할 필요없이 한번에 계산이 가능하다.