Logistic Regression

Logistic Regression

회귀를 사용하여 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류해주는 지도 학습 알고리즘이다.

x1(hours)	x2(attendance)	y(score)
10	5	90
9	5	80
3	2	50
2	4	60
11	1	40

공부시간에 따라 선형 회귀식을 적용하면 아래와 같은 모양이 나온다.

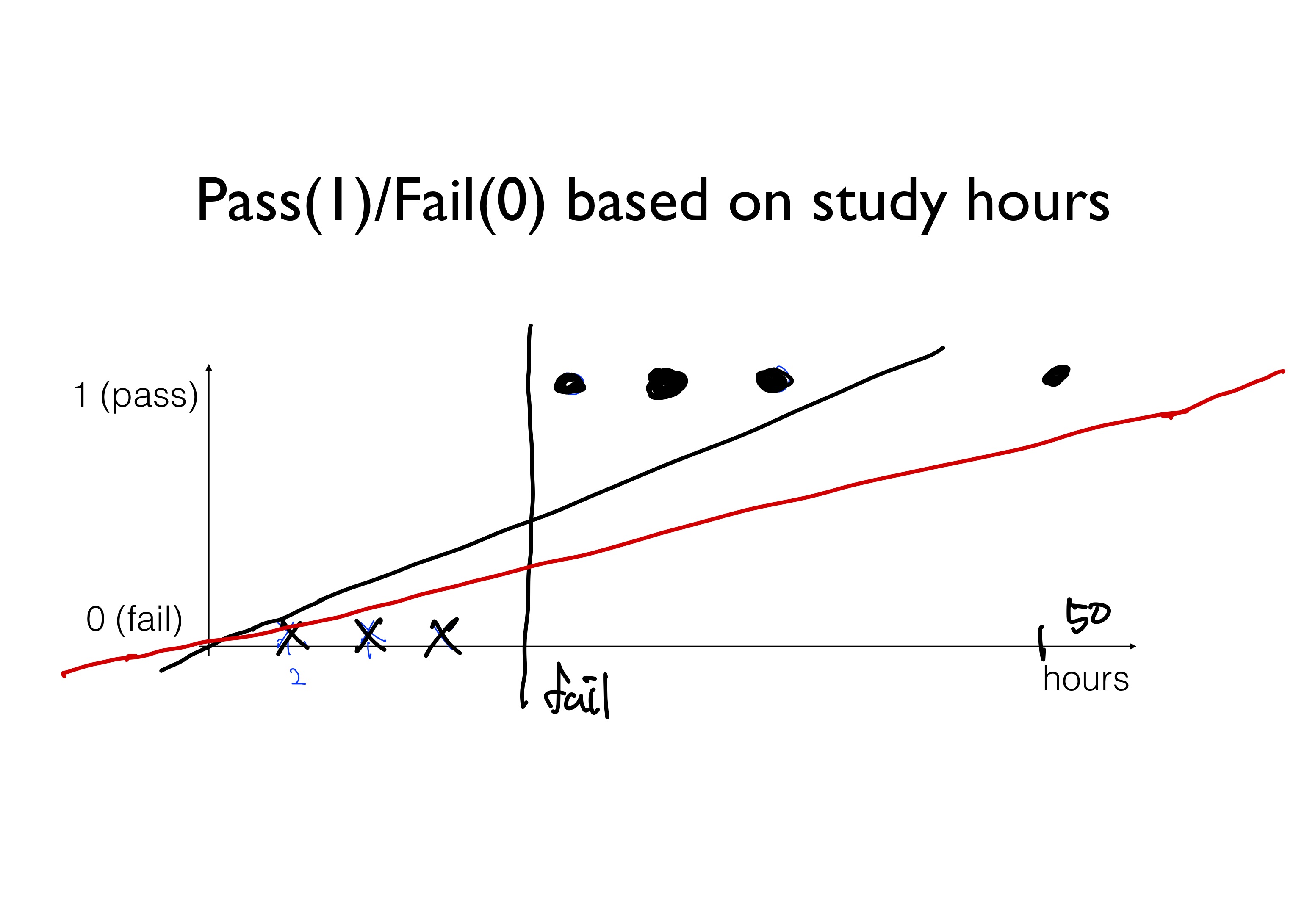
공부한 시간에 따라 합격할 확률이 달라진다.

근데 만약 기존 선형회귀에서 50시간을 공부한 사람이 추가된다고 가정하자

선형 모델을 학습시키면 cost를 최소화 하기위해서 기울기가 감소할 것 이다.

이전에 세워놓았던 합격과 불합격을 구분하는 기준선이 변하며 합격과 불합격을 정확하게 예측하지 못하는 상황이 발생한다.

또한 classification에서는 값이 0과 1이 되어야 한다.

하지만 linear한 가설 H(x) = Wx +b 를 가지게 된다면 0보다 훨씬 작거나 1보다 훨씬 큰 값이 나오게 된다.

Hypothesis

\[Z= Wx\\ H(x)=g(z)\\ H(x) = {1\over 1+ e^{-w^TX}}\]

sigmoid

로지스틱 회귀분석에서는 sigmoid를 사용하여 데이터를 성공과 실패로 분류한다.

아웃풋 범위 : 0~1

미분결과를 아웃풋의 함수로 표현 가능

logistics cost

\[Cost(W) {1 \over m} \sum c(H(x),y)\\ \\ C(H(x),y) = \begin{cases}-log(H(x)) : y=1 \\ -log(1-H(x)) : y=0 \end{cases} \\ \\\] \[Y=1\\ H(x)=1 : cost(1) =0 \\ H(x)=0 : cost=∞\] \[Y=0 \\ H(x)=0 : cost=0 \\ H(x)=1 : cost=∞\]

승산

범주 0에 속할 확률 대비 범주 1에 속활 확률

\[Odd= {p\over 1-p} \\ p=1 \quad odd= ∞ \\ p=0 \quad odd=0\]

로지스틱회귀에서

\[Odds = {\pi(X=x)\over 1-\pi(X=x)}\]

이고 분자가 1일때의 확률 분모가 0일때의 확률이 된다.

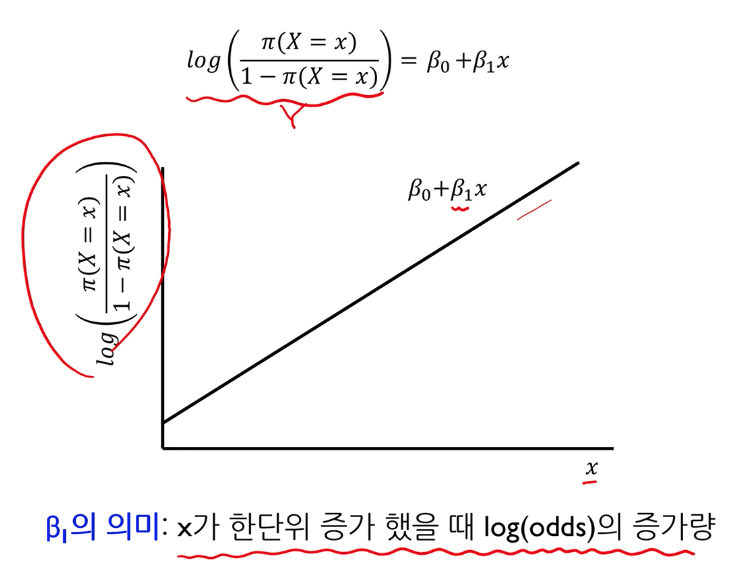
로짓 변환

선형으로 변하게 된다.

그래프로