softmax

Softmax

로지스틱회귀를 통해 2개의 선택지 중에서 1개를 고르는 이진분류를 풀어보았습니다.

이번에는 3개의 선택지에서 1개를 고르는 다중 클래스 분류 문제를 위한 소프트맥스 회귀를 알아보겠습니다.

Multinomial classification

x1(hours)	x2(attendance)	y(grad)
10	5	A
9	5	A
3	2	B
2	4	B
11	1	C

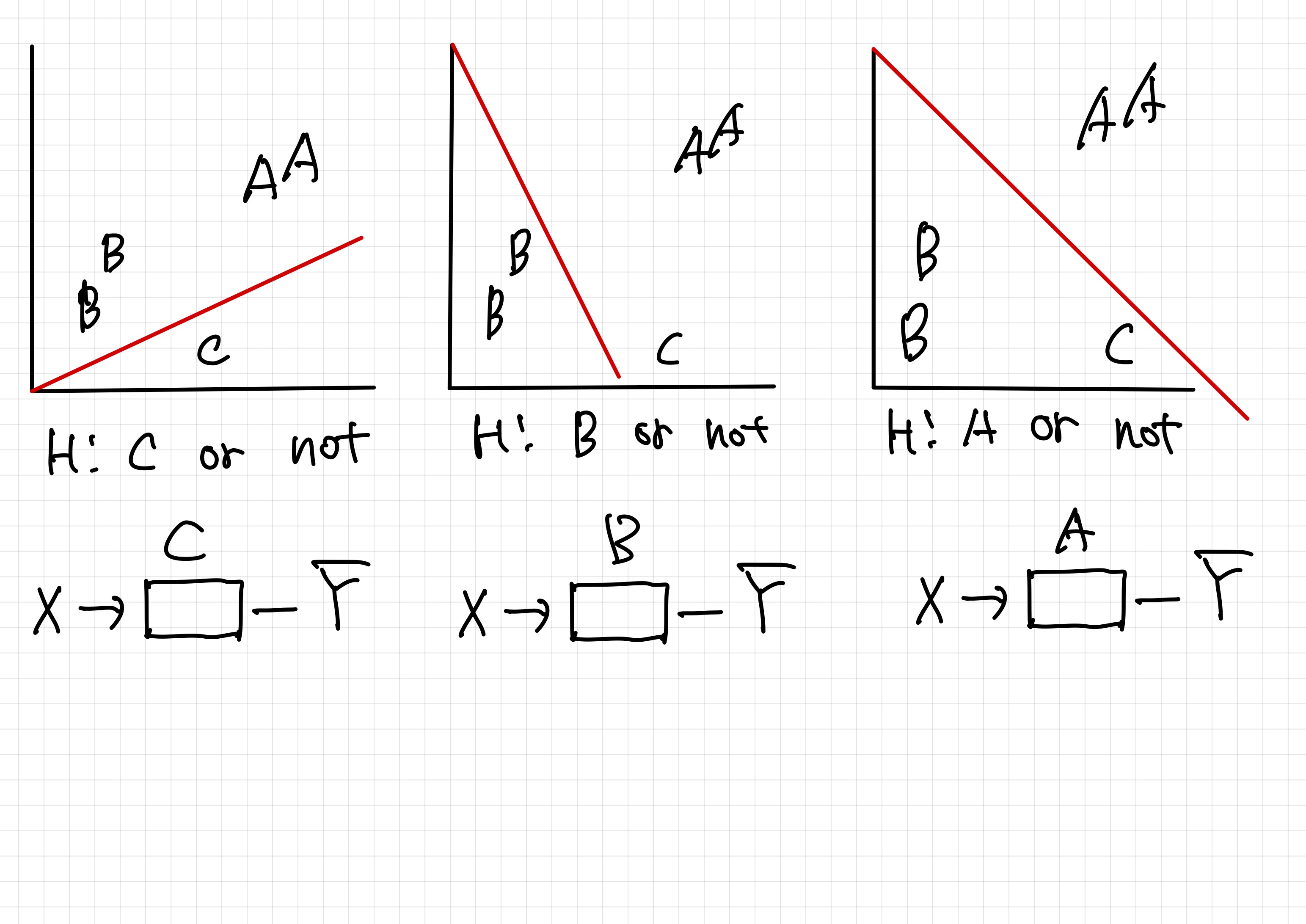
3개의 독립된 classfication으로 분류가 가능하다

독립된 형태의 벡터를 가지고 계산을 해서 값을 구한다

\[A : \begin {bmatrix} W_1\ W_2 \ W_3 \end{bmatrix} \begin{bmatrix} X_1\\ X_2 \\ X_3 \end{bmatrix}=[W_1X_1+W_2X_2+W_3X_3] \\ B : \begin {bmatrix} W_1\ W_2 \ W_3 \end{bmatrix} \begin{bmatrix} X_1\\ X_2 \\ X_3 \end{bmatrix}=[W_1X_1+W_2X_2+W_3X_3] \\ C : \begin {bmatrix} W_1\ W_2 \ W_3 \end{bmatrix} \begin{bmatrix} X_1\\ X_2 \\ X_3 \end{bmatrix}=[W_1X_1+W_2X_2+W_3X_3]\]

독립적인 계산을 간단하게 하기 위해서 저번시간에 말했던 Matrix 를 활용한다

\[\begin {bmatrix} W_{A1}\ W_{A2} \ W_{A3}\\ W_{B1}\ W_{B2} \ W_{B3}\\ W_{C1}\ W_{C2} \ W_{C3} \end{bmatrix} \begin {bmatrix} X_1\\ X_2\\ X_3 \end{bmatrix} = \begin {bmatrix} W_{A1X1}\ W_{A2X2} \ W_{A3X3}\\ W_{B1X3}\ W_{B2X2} \ W_{B3X3}\\ W_{C1X3}\ W_{C2X2} \ W_{C3X3} \end{bmatrix} =\begin {bmatrix} \bar {Y_A}\\ \bar{Y_B} \\ \bar{Y_C} \end{bmatrix}\]

앞 예제를 사용하여 계산하면

\[\begin {bmatrix} \bar {Y_A}\\ \bar{Y_B} \\ \bar{Y_C} \end{bmatrix}= \begin{bmatrix} 2 \\ 1\\ 0.1 \end{bmatrix}\]

이렇게 나온 결과값을 가지고 각각의 값에 시그모이드를 적용하면 확률을 구할 수 있다

하지만 이렇게 구한 확률은 각 클래스에 대한 확률이지 모든 클래스에 대한 확률이 아니다

모든 값을 더해주었을 때 1이 아니다

이럴 때 사용하는게 소프트맥스 함수이다

소프트맥스 함수는 선택해야 하는 선택지의 총 개수를 k라고 할 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정합니다

\[Y \begin{bmatrix} 2 \\ 1\\ 0.1 \end{bmatrix} \to S(y_i) = {e^{y_i} \over \sum_{j} e^{y_j}} \to probabilities \begin{bmatrix} 0.7 \\ 0.2\\ 0.1 \end{bmatrix}\]

cost function

예측값을 $S(y)$ 라고 하고 실제 값을 $Y$ 라고 했을 때 cost 함수는

\[D(S,L) = -\sum_{i} L_i log(S_i)\] \[-\sum_{i} L_i log(S_i)=-\sum_{i}L_i * log(\bar Y).png)\]

예를 들어 A와 B가 있다고 가정한다 \(Y= \begin{bmatrix} 0\\1 \end{bmatrix} =b\)

실제 값이 b라고 하였을 때

예측값이 B라고 가정하였을 때

\[\begin{bmatrix} 0\\1 \end{bmatrix}\ \odot -log \begin{bmatrix} 0\\1 \end{bmatrix}=\begin{bmatrix} 0\\1 \end{bmatrix} \ \odot \begin{bmatrix} \infty \\0 \end{bmatrix} = \begin{bmatrix} 0\\0 \end{bmatrix} \Rightarrow 0\]

cost가 0이 나오게 만들었다

만약 예측값이 A라고 가정하면

\[\begin{bmatrix} 0\\1 \end{bmatrix}\ \odot -log \begin{bmatrix} 1\\0 \end{bmatrix}=\begin{bmatrix} 0\\1 \end{bmatrix} \ \odot \begin{bmatrix} 0 \\ \infty \end{bmatrix} = \begin{bmatrix} 0\\ \infty \end{bmatrix} \Rightarrow \infty\]

cost 가 무한대가 나온다

Logistic cost와 cross entropy를 비교하면

\[C(H(x),y) = -ylog(H(x))-(1-y)log(1-H(x))\\D(S,L) = -\sum_{i} L_i log(S_i)\]

똑같은 값이 나오게 된다

이유는 두개의 예측 및 결과만 있기 때문이다.