MDP를 알 때의 플래닝
MDP 알 때의 플래닝
플래닝 : 어떤 상태 s 에서 액션 a를 실행하면 다음 상태가 어떻게 정해지는지 ,보상이 어떻게 될지 미리 알고 있을 때 정책을 개선해 나가는 과정
테이블 기반 방법론 : 모든 상태 s 혹은 상태와 액션의 페어(s,a)에 대한 테이블을 만들어서 값을 기록해 놓고, 그 값을 조금씩 업데이트하는 방식
밸류 평가하기 - 반본적 정책 평가
테이블의 값들을 초기화한 후, 벨만 기대 방정식을 반복적으로 사용하여 테이블에 적어 놓은 값을 조금씩 업데이트해 나가는 방법론이다.
| 출발 | s1 | s2 | s3 |
|---|---|---|---|
| s4 | s5 | s6 | s7 |
| s8 | s9 | s10 | s11 |
| s12 | s13 | s14 | 종료 |
4방향 랜덤이라는 정책 함수 $\pi$ 가 주어졌고 이때 각 상태 s 에 대한 가치 함수 v(s) 를 구하는 전형적인 prediction 문제
보상은 어느 액션을 하든 -1 이므로 $r_s^a$ 와 전이 확률 $p_{ss’}^a$을 알고 있다.
1. 테이블 초기화
| 0.0 | 0.0 | 0.0 | 0.0 |
|---|---|---|---|
| 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
정답과 멀수록 업데이트 횟수가 더 많이 필요하기 때문에 적당한 값인 0으로 촉기화한다.
2. 한 상태의 값을 업데이트
16개의 값들 중 1개의 값에 대해 업데이트를 진행
| 0.0 | 0.0 | 0.0 | 0.0 |
|---|---|---|---|
| 0.0 | -1 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
벨만 방정식 2단계를 사용하여 현재 상태 s의 가치를 다음에 도달하는 s’으로 표현
\[v_\pi(s) = \sum_{a \in A} \pi (a|s)(r_s^a + \gamma \sum_{s' \in s} P_{ss'}^a v_\pi(s')\]| 정책함수는 4방향으로 균등하게 랜덤하므로 $\pi (a | s) = 0.25$ 이고 $r_s^a = -1$ 이다. |
따라서 테이블의 $s_5$를 -1로 업데이트
‘종료 상태’의 경우 가치가 0으로 초기화 되는데 마지막 상태에는 미래라는 것이 존재하지 않기 때문이다.
3. 모든 상태에 대해 2의 과정을 적용
| -1 | -1 | -1 | -1 |
|---|---|---|---|
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | 0.0 |
4. 앞의 2~3번 과정을 계속해서 반복
이러한 과정들을 계속 반복하다보면 상태의 값이 어떤 값에 수렴하게 된다.
최고의 정책 찾기 - 정책 이터레이션
정책 이터레이션 : 기본적으로 정책 평가와 정책 개선을 번갈아 수행하여 정책이 수렴할 때까지 반복하는 방법론이다.
반복적 정책 평가를 통해 각 상태에 대한 밸류를 구했다.
이미 밸류 값을 알기 때문에 특정 상태에서 다음 상태로 갈때 가치가 떨어지거나 늘어나는지에 대해 알 수 있다.
그리디 정책 : 어떠한 상태에서 바로 다음 상태의 가치로만 판단하여 정책을 새우는 방식
모든 상태에 대해 그리디 정책을 선택하면 기존에 세웠던 정책에 비해 개선 된다.
평가와 개선의 반복
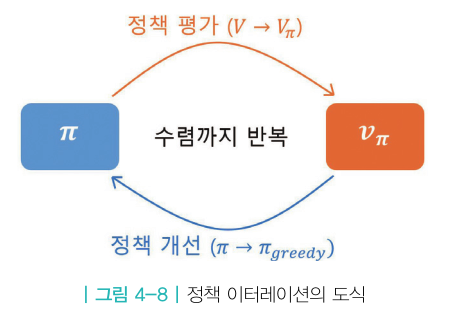
정책 평가 → 정책 개선
정책 평가 : 고정된 $\pi$ 에 대해 각 상태의 밸류를 구한다.$\pi$를 따랐을 때 각 상태의 밸류를 평가하는 일이기 때문에 정책 평가라고 부른다. 반복적 정책 평가를 사용한다.
정책 개선 : v(s)를 이용해 v(s)에 대한 그리디 정책을 시행한다.
정책 평가와 정책 개선을 계속해서 진행하다보면 최적 정책과 최적 가치가 나오게 된다.
정책의 개선
$\pi_{greedy}$ : 딱 한 칸만 그리디 정책으로 움직이고 나머지 모든 칸은 원래 정책으로 움직이는 정책
$\pi$ : 원래 정책
평균적인 리턴을 계산하였을 때 $\pi_{greedy}$ 가 크기 때문에 더 좋은 정책이다
정책 평가 간소화
업데이트를 6번하고 그리드 정책을 시행하나 업데이트를 무한번 시행하고 그리드 정책을 시행하나 최고의 정책이 나오는 시점은 다를 수 있다.
가치 함수를 끝까지 학습 하지 않아도 된다
오로지 해당 단계에서 테이블의 값을 이용해 만든 그리디 정책이 현재의 정책과 아주 조금이라도 다르기만 하면 된다.
정책이 현재의 정책과 아주 조금이라도 다르면 일단 개선을 할 수 있기 때문이다.
최고의 정책 찾기 - 밸류 이터레이션
최적 정책이 만들어내는 최적 밸류를 찾는 것
밸류 이터레이션 또한 테이블 기반 방법론을 사용한다.
| 0.0 | 0.0 | 0.0 | 0.0 |
|---|---|---|---|
| 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
| 0.0 | 0.0 | 0.0 | 0.0 |
최적 가치 테이블을 만든다.
\[v_*(s) = \underset{a}{max}[r_s^a + \gamma \sum_{s' \in s} P_{ss'}^a v_*(s)]\]$v_(s_5) = max$(-1+ 1.00,-1+ 1.00,-1+ 1.00,-1+ 1.0*0) = -1
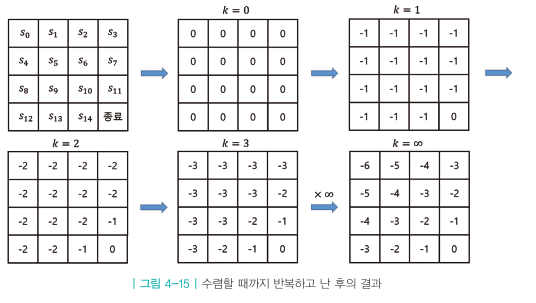
이 값은 각 상태의 최적 밸류를 의미한다.
MDP를 모두 아는 상황에서는 최적 밸류를 알면 최적 정책을 곧바로 얻을 수 있다.

Leave a comment