마르코프 결정 프로세스

마르코프 프로세스

마코프 특성을 지니는 이산시간 확률이다.

어떤 상태가 일정한 간격으로 변하고 다음 상태가 현재 상태에만 의존하며 확률적으로 변하는 상태 변화이다.

상태 전이 : 현재 상태에서 다음 상태로 넘어가는 것

하나의 상태에서 뻗어 나가는 화살표의 합은 항상 100%이다.

\[MP \equiv (S,P)\]

• 상태의 집합 S

  가능한 상태들을 모두 모아놓은 집합

• 전이 확률 행렬 P

  전이 확률 $P_{ss’}$는 상태 $S$에서 상태 $S’$ 에 도착할 확률을 가리킨다.

조건부 확률로 나타내면

\[P_{ss'} = P[S_{t+1}= s'|S_t=s]\]

마르코프 프로세스는 정해진 간격으로 상태가 바뀌기 때문에 해석하면 시점 t에서 상태가 s였다면 t+1 에서의 상태가 s’ 이 될 확률이다

전이 확률이라고 하지 않고 전이 확률 행렬이라고 하는 이유

$P_{ss’}$ 값을 각 상태 $s$ 와 $s’$ 에 대해 행렬이 형태로 표현 할 수 있기 떄문이다.

마르코프 성질

$P[S_{t+1}|S_t]=P[S_{t+1}| S_1,S_2, …,S_t]$ 미래는 오로지 현재에 의해 결정 된다

$S_{t+1}$이 될 확률을 계산하려면 현재의 상태 $S_t$가 무엇인지만 주어지면 충분하고 $S_t$ 이전에 방문했던 상태들 $S_1,S_2,….,S_{t-1}$ 에 대한 정보는 중요하지 않다

마르코프 리워드 프로세스(MRP)

마르코프 프로세스에 보상의 개념이 추가되면 MRP 가 된다.

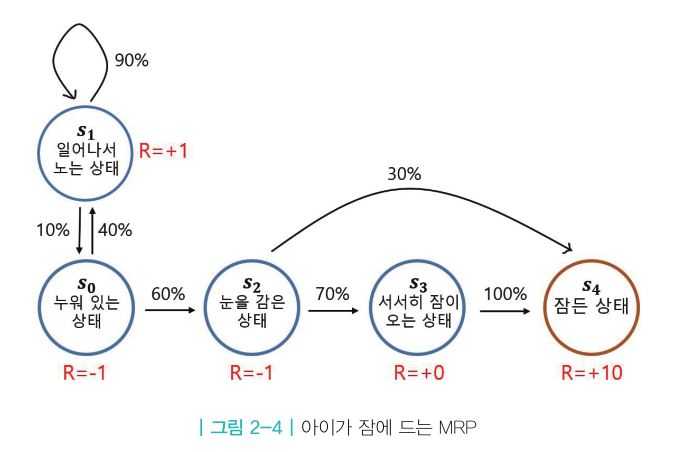
어떤 상태에 도착하게 되면 그에 따르는 보상을 받게 되는 것이다.

MRP 를 정의하기 위해서는 $R$(보상 함수)과 $\gamma$ (감쇠 인자)라는 2가지의 요소가 추가로 필요하다

\[MRP \equiv (S,P,R,\gamma)\]

• 상태의 집합 $S$
  • 마르코프 프로세스의 S와 같고, 상태의 집합이다.
• 전이 확률 행렬 $P$
  • 마르코프 프로세스의 P와 같고, 상태 s 에서 상태 s’ 으로 갈 확률을 행렬의 형태로 표현
• 보상 함수 $R$
  • R 은 어떤 상태 s에 도착했을 때 받게 되는 보상을 의미합니다.
  \[R = E[R_t| S_t =s]\]

  특정 상태에 도달했을 때 받는 보상이 매번 조금씩 다르기 때문에 기댓값을 사용한다.

• 감쇠 인자 $\gamma$
  • $\gamma$ 는 0 에서 1사이의 숫자이다.
  • 강화 학습에서 미래 얻을 보상에 비해 당장 얻는 보상을 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터이다
  • 미래에 얻을 보상의 값에 $\gamma$ 를 여러 번 곱해지며 그 값을 작게 만드는 역할을 한다.

감쇠된 보상의 합 ,리턴

MRP 에서는 MP와 다르게 상태가 바뀔 때마다 해당하는 보상을 얻습니다.

\[S_0,R_0,S_1,R_1,...,S_T,R_T\]

강화학습에서는 이러한 과정을 에피소드라고 한다.

이러한 표기법을 사용하여 리턴 $G_t$를 정의한다. 리턴이란 t 시점부터 미래에 받을 감쇠된 보상의 합이다

\[G_t=R_{t+1}+ {\gamma}R_{t+2} + {\gamma^2}R_{t+3} + \bullet\bullet\bullet\]

현재 타임 스텝이 t 라고 하였을 때 t 이후에 발생하는 모든 보상의 값을 더한 것이다

$\gamma$ 가 0~1 사이의 실수이기 때문에 여러번 곱해지면 값이 0에 가까워진다.

강화학습은 보상을 최대화 하도록 학습하는 것이 아니라 리턴을 최대화 하기 위한 것이다.

$\gamma$ 의 필요성

• 수학적 편리성
  • 리턴 $G_t$가 무한의 값을 가지는 것을 방지한다.
  • 리턴을 무한대로 잡는것보다 특정 값에 수렴하도록 잡는게 예측하기 쉽다.
• 사람의 선호 반영
  • 에이전트가 눈앞의 보상을 더 선호할 수 있다.
• 미래에 대한 불확실성 반영
  • 미래 가치에 대한 불확실성을 반영한다

밸류 평가

상태의 가치를 평가 하고 싶을 때 가장 먼저 떠오르는 방법은 보상이 높을 수록 좋은 상태

이전에 받은 보상 vs 이후에 받을 보상

어떠한 상태를 평가할 때는 그 시점으로 부터 미래에 일어날 보상을 기준으로 평가해야한다.

상태를 평가할 때 그 상태에서부터의 리턴을 측정하면 된다.

하지만 리턴은 값이 매번 바뀐다는 문제가 있어 밸류 평가를 할 때 리턴의 기댓값을 사용하면 된다.

에피소드 샘플링

샘플을 뽑아 온다는 뜻이다.

하나의 에피소드 안에서 방문하는 상태들이 매번 다르다. 그리고 그에 따라 리턴도 달라집니다.

에피소드에서 방문하는 상태들이 매번 다르다라는 표현을 강화학습의 용어에서 말하면 어떻게 샘플링 되냐는 말과 같다.

샘플링을 통해 어떤 값을 유추하는 방법론인 Monte-Carlo 접근법을 사용한다.

각 상태에서 다음 상태를 샘플링하여 진행하다보면 에피소드가 끝이나고 이러한 작업을 반복하다보면 우리는 에피소드의 샘플을 얻을 수 있다.

상태 가치 함수

상태를 인풋으로 넣으면 그 상태의 밸류를 아웃풋으로 출력하는 함수이다.

에피소드마다 리턴이 다르기 떄문에 어떤 상태 $S$의 밸류 $V(s)$ 는 기댓값을 이용하여 정의한다.

\[v(s) = E[G_t|S_t=s]\]

시점 t 에서 상태 s 부터 시작하여 에피소드가 끝날 때까지의 리턴을 계산해라

마르코프 결정 프로세스(MDP)

MRP 에 에이전트가 더해진 것이다

MDP 를 정의하기 위해서는 액션의 집합 A 가 추가되어야 한다.

\[MDP \equiv (S,A,P,R,\gamma)\]

• 상태의 집합 $S$
  • MP와 MRP 에서의 S 와 같다.
• 액션의 집합 $A$에
  • 에이전트가 취할 수 있는 액션들의 집합
• 전이 확률 행렬 $P$
  • 현재 상태가 $S$ 이며 에이전트가 액션 $A$ 를 선택했을 때 다음 상태가 $S’$이 될 확률

  • 액션 실행 후 도달하는 상태 $S$’ 에 대한 확률 분포

    \[P^a_{ss'} = P[S_{t+1}=s' | S_t=s ,A_t=a]\]
• 보상 함수 $R$

  • 기댓값을 사용하여 표시

    \[P^a_s=E[R_{t+1} |S_t=s,A_t=a]\]
• 감쇠 인자 $\gamma$
  • 미래에 얻을 보상의 값에 $\gamma$ 를 여러 번 곱해지며 그 값을 작게 만드는 역할을 한다.

정책 함수와 2가지 가치 함수

정책 함수 : 각 상태에서 어떤 액션을 선택할지 정해주는 함수이다.

\[\pi(a|s) = P[A_t=a \ S_t=s]\]

각 상태에서 할 수 있는 모든 액션의 확률 값을 더하면 1이 되어야 한다.

더 큰 보상을 얻기 위해 계속해서 정책을 교정해 나가는 것이 강화학습이다.

상태 가치 함수

가치 함수는 어떤 상태를 평가하고 싶다는 의도에서 출발

에이전트의 정책 함수에 따라 리턴이 달라진다.

$\pi$ 가 주어졌다고 가정했을 때 정책 함수는

\[v_\pi(s)= E_\pi [r_{t+1} + {\gamma}r _{t+2} + {\gamma^2}r_{t+3} +.. |S_t=s] = E_\pi [ G_t|S_t =s]\]

액션 가치 함수

액션 가치 함수는 $q(s,a)$ 로 표현하며 함수에 상태와 액션이 모두 인풋으로 들어가야한다.

\[q_\pi(s,a) = E_\pi[G_t|S_t =s ,A_t=a]\]

Prediction and Control

1. Predction : $\pi$ 가 주어졌을 때 각 상태의 밸류를 평가하는 문제
2. Control : 최적 정책 $\pi^*$ 를 찾는 문제