MDP를 모를 때의 플래닝

MDP를 모를 때의 플래닝

모델 프리(model-free)는 보상 함수($r_s^a)$와 전이 확률 ($p_{ss’}^a$)을 알수 없는 문제다.

“모델을 모른다.” , “MDP를 모른다.” , “모델 프리다” 같은 말로 이해하면 된다.

몬테카를로 학습

몬테카를로 학습(이하 MC)은 시행을 반복하고 특정 결과에 대한 평균을 구하면 특정한 결과의 기댓값이 되고, 시행을 무수히 반복한다면 한 값으로 수렴하게 된다는 사실을 이용한 방법론이다.

MDP에서 몬테카를로 방법론을 적용하는 방식은 환경에 에이전트를 가져다 놓고 학습을 시켜 에피소드가 종료할 때 까지 얻었던 리턴을 들에 평균을 구하는 방식이다.

몬테카를로 학습 알고리즘

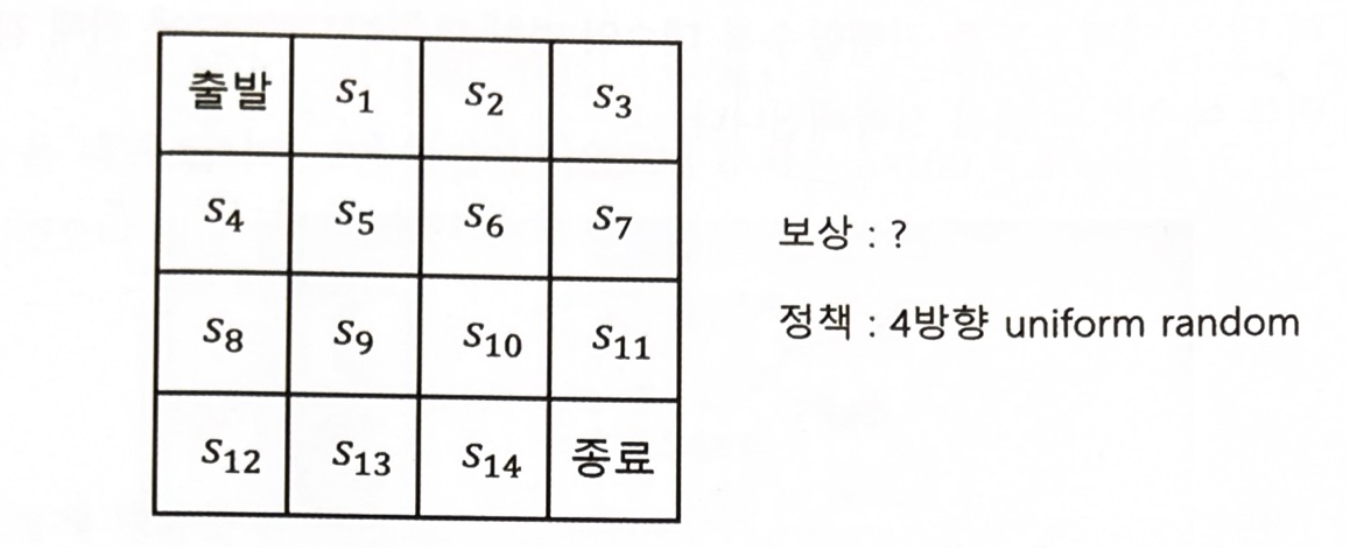
$r_s^a$와 $p_{ss}^a$를 모르지만 실제 MDP에는 고정된 $r_s^a$와 $P_{ss}^a$가 있다.

실제로 액션을 해보는 것이 아니라 에이전트가 할 수 있는 모든 액션에 대해 액션을 선택하는 확률

$\pi(a

s)$ 에다가 $v(s’)$ 을 곱하여 기존 상태의 가치를 구한다.

1. 테이블 초기화

N(s) : s를 총 몇번 방문했는지에 대해서, V(s)는 해당 상태에서 경험했던 리턴을 계산하기 위해서

1. 경험 쌓기

$S_o$부터 시작하여 $a_0$를 정하고 그에 따른 보상을 받고 다음 스테이트로 이동한다.

에이전트가 종료 지점에 도달하기까지의 에피소드는 다음과 같이 표현할 수 있다.

\[s_0,a_0,r_0,s_1,a_1,r_1... s_{r-1},a_{r-1},r_{r-1},s_r\]

각 상태에 대한 리턴을 계산한다.

\[G_0=r_0+\gamma r_1+ \gamma^2 r_2+... \gamma ^{T-1} r_{T-1} \\ G_1=r_1+ \gamma r_2...+ \gamma^{T-2} r_{T-1} \\ ... \\ G_T=0\]

1. 테이블 업데이트

   

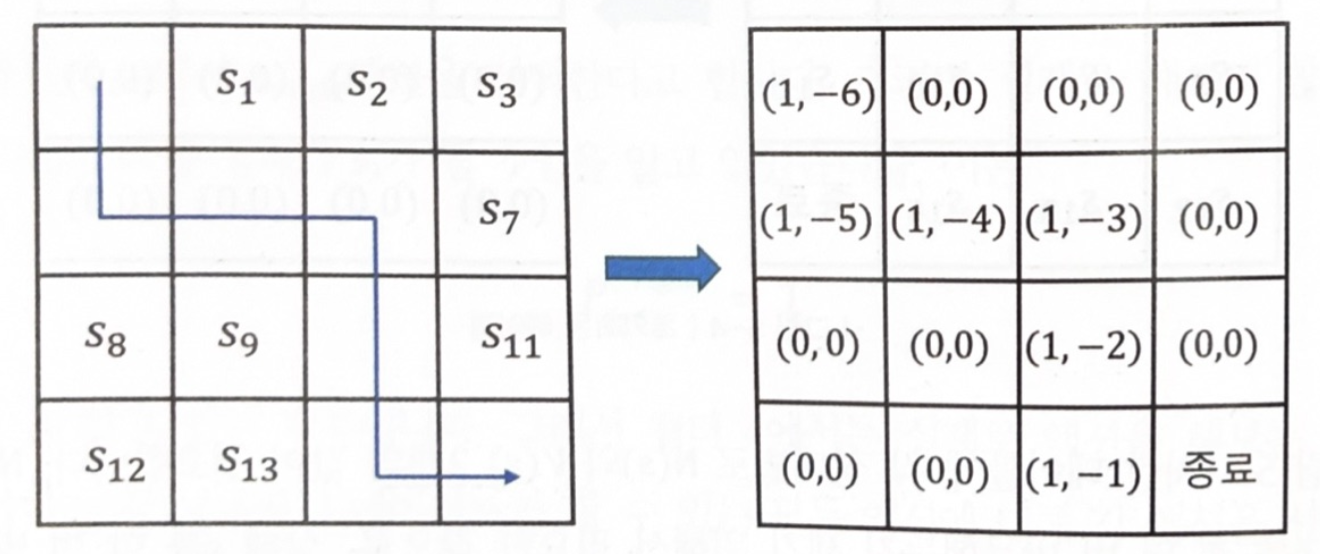
에피소드에서 방문했던 모든 상태에 대해 해당 칸의 N(s)와 V(s)값을 업데이트 합니다.

\[N(s_t)\leftarrow N(s_t)+1 \\ V(s_t)\leftarrow V(s_t)+G_t\]

모든 상태에 대한 보상은 -1이고 감마는 1로 계산된다.

1. 밸류 계산

충분히 경험했다고 판단하면 리턴의 평균을 구한다.

\[v_{\pi}(s_t) \cong {v(s_t)\over N(s_t)}\]

모든 상태 s 에 대해 리턴의 합 V(s)를 방문 횟수 N(s)로 나누면 각 상태의 밸류에 대한 근사치이다.

조금씩 업데이트하는 버전

\[V(s_t) \leftarrow (1-\alpha) * V(s_t) + \alpha *G_t\]

에피소드가 1개 끝날 때마다 테이블의 값을 조금씩 업데이트하는 버전이다.

$\alpha$의 값이 클수록 한 번에 더 크게 업데이트하고 ,작을 수록 더 조금씩 업데이트 한다.

Temporal Difference 학습

Temporal difference(이하 TD)는 미래의 리턴을 예상해서 현재의 리턴을 업데이트하는 방법론이다.

추측을 추측으로 업데이트하는 방식이다. 예를 들어 일요일에 비가 올 확률을 예측할 때 금요일에는 50%라고 예측을 했는데 토요일에 예측한 확률이 80%이면 금요일의 예측 값을 조금 더 높여주는 방식이다.

여기서 의문이 하나 생길 것이다. ‘다음 날의 추측이 더 정확하란 법이 있을까?’

이에 대한 근거는 $G_t$는 $v_{\pi}(s_t)$의 불편 추정량 이기 때문에 $G_t$의 평균은 $v_\pi (s_t)$로 수렴하기 때문이다.

TD가 성립되는 이유는 미래의 리턴과 현재의 리턴을 여러 개 모아서 기댓값을 구하면 실제값에 다가가게 되며, 이때 목표값을 TD 타깃이라 한다.

TD의 학습은 MC의 학습과 매우 유사하지만 다른점이 있다.

\[s_0\rightarrow s_1 \rightarrow s_2\rightarrow s_3\rightarrow s_4 \rightarrow... s_{11} \rightarrow 종료\]

MC는 종료 상태에 도달하여 테이블을 업데이트 하지만 TD는 각 상황에서 테이블을 업데이트 한다는 점이다.

수식으로 비교해보면 다음과 같다.

\[MC : V(s_t) \leftarrow V(s_t) +\alpha (G_t-V(s_t)) \\ TD : V(s_t) \leftarrow V(s_t) + \alpha (r_{t+1}+\gamma V(s_{t+1})-V(s_t))\]

몬테카를로 vs TD

여러 측면에서 두 개의 방법론을 비교해보자

학습 시점

• Episodic MDP

  MDP의 상태들 중에 종료 상태라는 것이 있어서 에이전트의 경험이 에피소드 단위로 나뉘어질 수 있는 것

• Non-Episodic MDP

  종료 상태 없이 하나의 에피스도가 무한이 이어지는 MDP

MC는 Episodic MDP에만 적용이 가능하고 TD는 둘다 적용이 가능하다.

분산

MC는 리턴을 통해 업데이트가 진행된다. 리턴을 구하기 위해서는 에피소드 하나가 끝나야 하는데 똑같이 액션을 해도 하나의 에피소드를 학습하는데 걸리는 시간은 정해져 있지 않다.

결론적으로 MC는 분산의 변동성이 매우 크다.

TD는 하나의 샘플만 보면 바로 업데이트가 가능하기 때문에 분산이 매우 작다.

몬테카를로와 TD의 중간

n스텝 TD

\[r_{t+1} + \gamma V(s_{t+1})\]

한 스텝만큼 진행하여 실제 보상을 관찰하고, 도착한 상태의 가치를 가치함수 V를 이용하여 추측한다.

하나의 스텝만 가서 평가하지말고 여러개의 스텝을 고려해보자

\[\begin{aligned} N=1& : r_{t+1} +\gamma V(s_{t+1}) \\ N=2& : r_{t+1} + \gamma V(s_{t+2}) +\gamma ^2 V(s_{t+2}) \\ N=n& : r_{t+1} + \gamma V(s_{t+2}) +\gamma ^2 V(s_{t+2})+ . . . + \gamma ^n V(s{t+n}) \end{aligned}\]

n-step 리턴에서 n이 무한으로 가면 결국 리턴이 된다.

결국 n이 무한대로 늘어나면 MC에 가까워지고 1이면 TD가 되는 것이다.

우리는 n의 적절한 값을 찾아야한다.